Chapitres

Exercice 1 : La grêle
La grêle se forme dans les cumulo-nimbus situés entre 1000 m et 10000 m d’altitude où la température est très basse, jusqu’à – 40 °C. Le grêlon tombe lorsqu’il n’est plus maintenu au sein du nuage. Au sol sa vitesse peut atteindre 160 km/h.
On étudie un grêlon de masse 13 g qui tombe d’un point O d’altitude 1500 m sans vitesse initiale. Il peut être assimilé à une sphère de diamètre 3,0 cm.

Le point O sera pris comme origine d’un axe Oz orienté positivement vers le bas.
L’intensité de la pesanteur sera considérée comme constante et de valeur go = 9,80 m.s-2.
Données :
Volume d’une sphère : \[ V = \frac {4} {3} \pi \times r^{3} \]
Masse volumique de l’air r = 1,3 kg.m-3
A – CHUTE LIBRE
On admettra que le grêlon tombe en chute libre
En appliquant la deuxième loi de Newton, déterminer les équations horaires
donnant la vitesse et la position du centre d’inertie G du grêlon en fonction de la
durée t de la chute.
Calculer la valeur de la vitesse lorsqu’il atteint le sol, ce résultat est-il
vraisemblable ? Justifier.
Chute réelle
En réalité le grêlon est soumis à deux autres forces, la poussée d’Archimède et la force de frottement fluide proportionnelle au carré de la vitesse telle que F = K×v².
Par une analyse dimensionnelle, déterminer l’unité du coefficient K dans le Système International.
Donner l’expression de la valeur de la poussée d’Archimède ; la calculer et la comparer à celle du poids. Conclure.
On néglige la poussée d’Archimède.
Établir l’équation différentielle du mouvement.
Montrer qu’elle peut s’écrire sous la forme \[ \frac {\text{d}v}{\text{d}t} = A - B \cdot v ^{2} \]
On veut résoudre cette équation différentielle par une méthode numérique : la méthode d’Euler.
Le tableau suivant est un extrait d’une feuille de calcul des valeurs de la vitesse (v) et de l’accélération (a) en fonction du temps (t). Il correspond aux valeurs
A = 9,80 m.s-2 et B = 1,56x10-2 m-1, pas de variation Dt = 0,5 s.
| t (s) | v (m.s-1) | a (m.s-2) |
|---|---|---|
| 0,00 | 0,00 | 9,80 |
| 0,50 | 4,90 | 9,43 |
| 1,00 | 9,61 | 8,36 |
| 1,50 | 13,8 | 6,83 |
| 2,00 | 17,2 | a4 |
| 2,50 | v5 | 3,69 |
| 3,00 | 21,6 | 2,49 |
Déterminer a4 et v5 en détaillant les calculs.

Exprimer littéralement la vitesse limite atteinte par le grêlon en fonction de A et
B puis calculer sa valeur numérique.
La courbe d’évolution de la vitesse en fonction du temps est donnée ci-dessous. Retrouver graphiquement la valeur de la vitesse calculée au paragraphe précédent.

Exercice 2 : Le bac à décantation
Étude de la chute d’une particule dans un liquide visqueux :
On prépare un mélange homogène constitué d’un liquide de masse volumique
rl = 1,0 x 103 kg.m-3 et de particules solides de forme sphérique de rayon R = 2,0 x 10–6 m,
de masse volumique rS = 1,5 x 103 kg.m-3 et de masse m = 5,0 x 10–14 kg.
On dépose, à la date t = 0 s, une fine couche (dont on néglige l’épaisseur) de ce mélange
homogène à la surface d’un récipient contenant le même liquide, à l’état pur, que le
mélange précédent.
A partir de cet instant, les particules, que l’on suppose initialement au repos, se déplacent verticalement vers le fond du récipient.
On suppose que la vitesse limite est suffisamment faible. Dans cette hypothèse, les
particules sont soumises à leur poids, à la poussée d’Archimède : \[ \overrightarrow{\Pi} = - \frac {4} {3} \cdot \pi \cdot R^ {3} \cdot \rho_ {l} \cdot \overrightarrow {g} \]
et à une force de frottement où f vaut 3,1 x 10–12 kg.s-1 et représente le coefficient de frottement.
On donne g = 9,8 N.kg-1.
Pour étudier le mouvement de la particule, on se place dans un repère unidimensionnel d’axe Oz vertical et dirigé vers le bas, d’origine O au niveau de la surface libre du liquide.
(voir annexe 1).
En effectuant une analyse dimensionnelle, vérifier que l’unité du coefficient de frottement est bien le kg.s-1.
Compléter l’annexe 1 en faisant figurer les forces s’exerçant sur la particule pendant sa chute à l’instant t.
En appliquant la deuxième loi de Newton, montrer que l’équation différentielle relative à la vitesse de la particule est :
\[ \frac {\text {dv}} {\text {dt} } + \frac {\text {f} } {\text {m} } \cdot \text {v} = \text {g} \cdot (\frac { \rho _ {s} - \rho _ {l} } { \rho _ {s} }) \]
En déduire que la valeur de la vitesse limite atteinte par les particules s’exprime par la relation :
\[v_{l} = \frac { \rho _ {s} - \rho _ {l} } { \rho _ {s} } \cdot \frac {\text {m} } {\text {f} } \cdot \text {g}\]
Calculer vl
La solution de l’équation différentielle établie à la question 1.3. est de la forme :
\[\text{v} (\text{t}) = \text{v} _ {l} \cdot (1 - e ^ {-\frac{\text{f}}{\text{m}} \cdot t} )\]
Déterminer la date t1 à partir de laquelle la valeur de la vitesse vaudra 99% de la
valeur de la vitesse limite.
Une étude expérimentale a permis d’obtenir le graphe, donné ci-après, représentant
les variations de la vitesse de la particule au cours du temps.
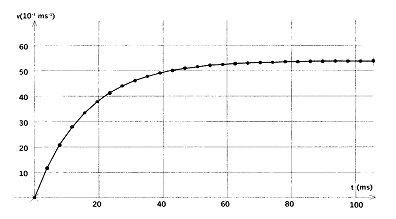
Déterminer par une méthode de votre choix le temps caractéristique t1 de l’évolution de la vitesse.
Décrire et nommer les phases du mouvement de la particule entre les instants t = 0 et t’ = 100 ms.
Application : modélisation simple d’un bac à décantation à flux horizontal.
Le principe d’un bac à décantation à flux horizontal consiste à faire circuler, à vitesse
constante v , un courant d’eau contenant des particules de masses différentes dans
un dispositif que l’on peut modéliser de la façon suivante :
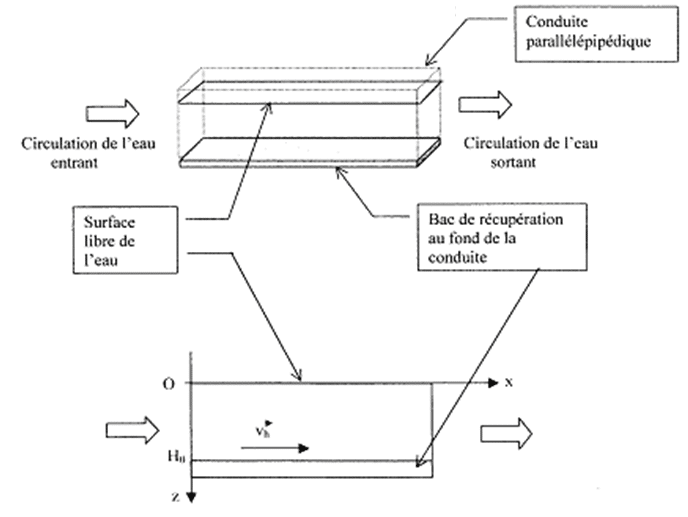
En fonction des caractéristiques des particules, ces dernières vont tomber au fond du bac en des endroits différents. On peut donc, par ce procédé, séparer les particules de nature différente contenues dans l’eau.
On s’intéresse au mouvement d’une particule (identique à celle de la partie 1) initialement à la surface de l’eau, à la côte z = 0 et pénétrant dans le bac en x = 0.
En imaginant que la particule reste à la surface de l’eau, quel temps t2 mettrait-elle pour parcourir la longueur du bac L = 1,0 m, si la vitesse de circulation d’eau est constante et de valeur vh = 0,10 m.s-1 ?
En comparant les valeurs de t1 (déterminé à la question 1.6.a.) et t2, justifier que l’on puisse considérer que la vitesse de la particule dans la conduite est (où vl est la valeur de la vitesse limite atteinte en chute libre dans le fluide).
On déduit de l’étude précédente les grandeurs cinétiques données en annexe 2 (à rendre avec la copie). Compléter la dernière ligne du tableau.
En déduire que la trajectoire z = f(x) est une droite de coefficient directeur :
\[\alpha = \frac {\rho _ {s} - \rho _ {l} } {\rho _ {s}} \cdot \frac {mg} {f \cdot v_{h}}\]
En réalité les particules ne sont pas toutes identiques et sont caractérisées par leur
masse m.
Calculer la valeur de la masse mC de la particule pour que cette dernière tombe dans le bac à récupération au point de coordonnées x = L et z = H0 = 0,54 m.
Dans quelle zone vont tomber les particules de masses m et de même masse
volumique rS :
- Si m < mC ?
- Si m > mC ?
Justifier votre réponse.

Annexes à rendre avec la copie
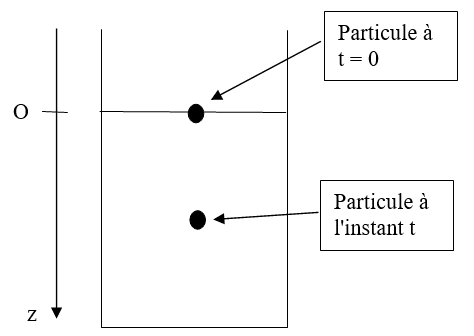
ANNEXE 3 (à rendre avec la copie)
| Projection selon Ox | Projection selon Oz | |
|---|---|---|
| Accélération | ax(t) = 0 | az (t) = 0 |
| Vitesse | vx (t) = vh | vz(t) = vl |
| Position | x(t) = | z (t) = |
Exercice 3 : Stocker l'énergie
Est-ce facile de stocker de l'énergie ? Certains penseront que cette question n'a pas d'intérêt : bien sûr qu'il est facile de stocker de l'énergie ! II suffit de disposer d'un tas de charbon dans la cave, d'une pile électrique, d'avoir un réservoir de fioul chez soi. Tout cela permet effectivement de disposer d'une réserve d'énergie que nous pouvons consommer quand nous le souhaitons.
Ce qui fait l'intérêt de l'énergie ce n'est pas seulement d'en avoir, c'est d'en avoir quand nous en avons besoin. Les énergies renouvelables (solaire ou éolienne), qui dépendent d'une source d'énergie (le Soleil ou le vent) qui n'est pas nécessairement disponible quand nous désirons qu'elle le soit, illustrent bien ce problème. Dès lors, il est nécessaire de pouvoir stocker de l'énergie.
Le but de cet exercice est d'étudier trois modes de stockage de l'énergie et de comparer dans chacun des cas l'énergie stockée par kilogramme, d'une part et le temps nécessaire pour l'accumuler et la délivrer, d'autre part.
Les quatre parties de cet exercice sont indépendantes.
L'énergie est stockée sous forme électrique puis une étincelle est produite lors de la restitution de cette énergie.
On souhaite stocker une énergie EL dans une bobine idéale d'inductance L.
On dispose d'une alimentation continue qui délivre une tension U = 6,0 V
À t= 0, on ferme l'interrupteur K.
1.1. À l'aide de la relation liant uL, L et i, déterminer la valeur de uL en régime permanent.
1.2. Montrer que l'expression de l'intensité du courant en régime permanent est I — .
1.3. Exprimer l'énergie EL emmagasinée par la bobine lorsque le régime permanent est atteint.
1.4. On souhaite que la bobine stocke l'énergie EL = 10 J en régime permanent. On dispose d'une résistance R égale à 1,8 O. Calculer alors la valeur de L pour satisfaire cette condition.
Stockage hydraulique de l'énergie
3. Stockage hydraulique de l'énergie
Les barrages hydroélectriques constituent des réserves d'eau dont l'énergie potentielle de pesanteur est utilisée pois faire tourner dos turbines génératrices d'électricité. Quand la demande d'énergie électrique sur le réseau est faible (heures creuses, week-end) la production excédentaire des dispositifs non réglables (nucléaire, solaire, éolien...) est utilisée pour remonter l'eau dans des barrages d'altitude. Pendant les pics de consommation, cette eau est relâchée â nouveau et permet la production de l'électricité.
3.1. Donner l'expression de l'énergie potentielle de pesanteur E,„:, de l'eau dans un barrage d'attitude en fonction de la masse volumique p de l'eau. de son volume V. de l'intensité de la pesanteur g et de la hauteur de chute h. On considère l'énergie potentielle de pesanteur nulle au niveau de la turbine et la hauteur de chute h constante.
3.2. La centrale de Grand Maison en Isère possède un réservoir de 140 millions de mètres cubes d'eau dont la hauteur de chute est h = 0,90 km.
On donne la masse volumique de Peau p= 1.0 x 103 kg.m3 et l'intensité du champ de pesanteur : g = 10 m.s-1. Déterminer l'énergie potentielle de pesanteur E, pouvant être stockée sous cette forme.

4. Comparaison de certaines des caractéristiques des trois dispositifs
Afin de comparer les différents modes de stockage des trois dispositifs étudiés, on donne, dans le tableau ci-dessous, la quantité d'énergie pouvant être stockée par kilogramme et le temps nécessaire pour récupérer cette énergie stockée.
| Bobine supraconductrice | Supercondensateur | Barrage | |
|---|---|---|---|
| Energie stockée par kg | 15 kJ | 20 kJ | 10 kJ |
| Durée minimale pour récupérer la quasi-totalité de l'énergie stockée. | 1 ms | 10 s | 10 jours |
| Puissance moyenne disponible par kg | 1,5 x 107 W | 2 x 103 W | P |
4.1. Calculer la puissance moyenne P disponible par kg pour le barrage.
4.2. On utilise des supercondensateurs dans les voitures électriques pour fournir un courant d'intensité élevée au démarrage. Le supercondensatour doit fourni une intensité constante égale 8 100 A sous une tension de 2.5 V pendant 10 s.
Calculer la masse du superoondensateur nécessaire pour fournir l'énergie souhaitée au démarrage du véhicule électrique.
Rappel : un générateur débitant un courant d'intensité I sous une tension Li fournit au circuit une puissance P = Ut






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !