Chapitres
Gradient en coordonnées cartésiennes
Le gradient est la généralisation de la notion de dérivée à plusieurs variables. En effet, lorsque nous avons étudié les dérivées, nous avons toujours dérivé par rapport à x. Cela fonctionne sur une fonction n'ayant qu'une seule variable. Seulement les fonctions à une variable sont un cas particulier. Nous pouvons tout à fait avoir des fonctions avec plus d'une seule variable. Dans ce cas-là, celles-ci ne se représentent pas sur un plan à 2 dimensions mais sur un plan à n dimensions. Il est par conséquent impossible de représenter graphiquement des fonctions à plus de 3 variables (on ne peut pas représenter des espaces à 4 dimensions ou plus). Pour ces dernières, nous utiliserons l'algèbre linéaire que nous verrons dans un autre cours. Par exemple, soient x,y,z 3 variables appartenant à R. Soit la fonction f telle que : f(x,y,z) = x² + 2xy + zx + 3xyz. La fonction f est définie et dérivable sur R et on note les dérivées partielles de f pour x,y,z comme suit :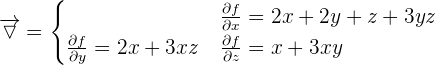 
Le gradient de la fonction f est noté 
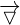. On remarque que quand l'on effectue les dérivées partielles par rapport à une variable, les autres variables sont quant à elles considérées comme des constantes. Il faut donc toujours faire très attention à la variable par rapport à laquelle on dérive. Il existe un lien entre le gradient et la différentielle totale d'une fonction. On note 
Par conséquent, pour revenir à notre exemple précédent, la dérivée totale de la fonction f est égale à : 
On peut également considérer la différentielle totale par le produit scalaire du gradient par le vecteur dr avec r étant le déplacement élémentaire de composante dx,dy,dz. On note dans ce cas :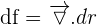 
Gradient en coordonnées cylindriques
En coordonnées cylindriques, on représente un point M différemment qu'en coordonnées scalaires. En effet, on caractérise un point M avec les coordonnées r,θ et z avec r étant le rayon du cylindre, θ l'angle polaire et z la troisième coordonnée du cylindre. A l'instar du gradient pour les coordonnées cartésiennes, on a la dérivée totale de la fonction cylindrique f qui est égale à : 
En revanche les composantes du gradient en coordonnées cylindriques diffèrent, et on a :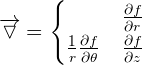 
Gradient en coordonnées sphériques
En coordonnées sphériques, on représente un point M différemment qu'en coordonnées scalaires. En effet, on caractérise un point M avec les coordonnées r,θ et φ avec r étant le rayon du cylindre, θ l'angle entre l'axe z et le rayon et φ étant l'angle entre l'axe x et la projection du rayon dans le plan x,y.Cet angle varie donc entre 0 et 2π en coordonnées polaires. A l'instar du gradient pour les coordonnées cartésiennes, on a la dérivée totale de la fonction cylindrique f qui est égale à : En revanche les composantes du gradient en coordonnées diffèrent, et on a :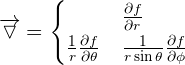 
Représentation graphique
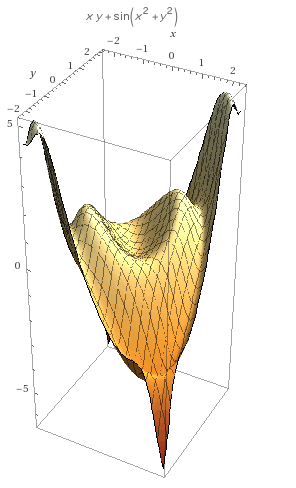
Pour chacune des 3 coordonnées, on peut représenter graphiquement les différentes fonctions associées tant que le nombre de variables n'est pas supérieur à 3. Pour les coordonnées cartésiennes, on utilise généralement les vecteurs unitaires 
avec le vecteur i représentant l'abscisse, le vecteur j représentant l'ordonnée et le vecteur k la profondeur (la 3ème dimension). En prenant pour exemple la fonction y = -3x + 4z on obtient alors une représentation graphique en 3 dimensions de cette fonction (voir début de l'article). Concernant la représentation d'une fonction en coordonnées cylindriques, on utilise les vecteurs unitaires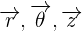 
avec le vecteur r représentant le rayon du cylindre, le vecteur 
l'angle du cylindre en coordonnées polaires et z la hauteur du cylindre. On peut par exemple dessiner ce cylindre avec les coordonnées cylindriques :
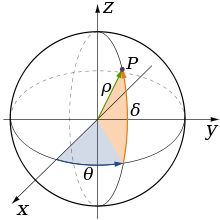
Enfin, concernant la représentation d'une fonction en coordonnées cylindriques, on utilise les vecteurs unitaires 
avec le vecteur p représentant la distance du point P au centre O, le vecteur l'angle sphérique orienté par les demi-plans et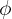 
l'angle non orienté par les vecteurs z et OP. On peut par exemple dessiner cette sphère avec les coordonnées sphériques :
Opérateur Nabla
Le nabla à l'instar du gradient peut s'écrire en coordonnées cartésiennes, cylindriques et sphériques. Concernant les coordonnées cartésiennes, on l'écrit comme suit : 
Concernant les coordonnées cylindriques, on écrit l'opérateur nabla comme suit : 
Enfin concernant les coordonnées sphériques, on écrit l'opérateur nabla de cette manière : 
Exercices Corrigés
Exercices
Exercice 1 : Calcul de dérivée totale Soit f la fonction définie par 
.
- Calculer le gradient de la fonction f
- Déterminer la dérivée totale de la fonction.
Exercice 2 : Gradient d'une fonction Soit une fonction f définie et dérivable dans le plan (O,x,y) tel que
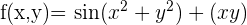
- Déterminer les coordonnées du gradient de f
- Déterminer les coordonnées du point gradient de M(-1;-3)
- Déterminer les coordonnées du point M(-1;-3)
- Déterminer la dérivée totale de f
Corrigés
Exercice 1 :
- f est définie et dérivable sur R. On détermine le gradient :
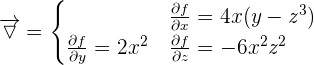
- Maintenant que l'on a déterminé le gradient de la fonction, on peut calculer la dérivée totale :
Exercice 2 : 1. f est définie et dérivable sur R. On détermine le gradient :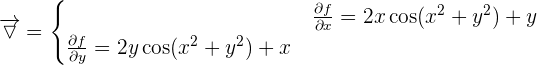 
2. 
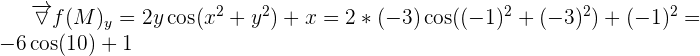
3. Pour les coordonnées du point M(-1,-3) pour la fonction f, il suffit simplement de remplacer x et y dans la fonction :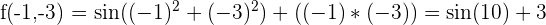 
4. email Pour obtenir la dérivée totale de f, on effectue la somme des dérivées partielles : 
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Je suis vraiment fier de vous découvrir, votre blog est vraiment super ! J’aime bien son interface, et j’ai trop adoré le contenu aussi. Surtout continuez ainsi !
[url=http://www.qualite-voyance.fr]voyance par mail gratuite[/url]