Chapitres
La fonction exponentielle est une fonction mathématique fondamentale exprimée par f(x) = e^x, où "e" est une constante approximativement égale à 2.71828. Cette fonction présente une croissance rapide et continue avec l'augmentation de "x".
🥼 Elle est utilisée pour modéliser des phénomènes de croissance exponentielle dans divers domaines tels que la finance, la biologie, la physique, etc.
- Le graphique de la fonction exponentielle présente une courbe ascendante sans point d'inflexion, et sa dérivée est elle-même
- Les propriétés clés incluent la propriété de l'addition des exposants et son rôle crucial dans la résolution d'équations et de problèmes mathématiques
Découvrez tout sur la fonction exponentielle réelle dans cet article !
Rôle de la fonction exponentielle ♾️
⚠️ Dans cet article, on étudiera uniquement l'exponentielle réelle, nous ne nous intéresserons pas à l'exponentielle complexe.
La fonction exponentielle est définie et continue sur : 
et est à valeur dans [ ]0;+\infty [ ]
On peut le noter :
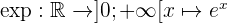
L'exponentielle de x est notée [e^x] ou [exp(x)].
La fonction exponentielle est dérivable sur et a pour dérivée elle même c'est à dire [(e^x)'=e^x] pour tout réel x. Cela implique bien entendu qu'une primitive de exp(x) est exp(x).
La fonction exponentielle est définie comme l'unique fonction telle que sa dérivée est elle-même et qui prend la valeur 1 lorsque x vaut 0.
Source Superprof
Montrons que cette fonction est unique
Supposons qu'il existe une fonction f dérivable sur
telle que f'=f et f(0)=1
Définissons une fonction h sur
telle que [h(x)=f(x)times f(-x)]
Pour tout réel x, on a :
- h(x)=f'(x)f(-x)+f(x)(-f'(x))=0
- Donc la fonction h est constante
- Comme h(0)=f(0)f(-0)=1, h(x)=f(x)f(-x)=1 et f ne peut pas s'annuler.
Supposons qu'il existe une fonction g telle que g'(x)=g(x) pour tout réel x et g(0)=1 :
- Comme f ne s'annule jamais, on peut poser
- On a
- Donc k est une fonction constante
- Or
- Donc
- D'où g(x)=f(x)
👉 La fonction exponentielle est donc strictement positive (d'après la démonstration ci-dessus), c'est à dire, pour tout réel x on a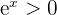 
De plus, elle est strictement croissante et croit très rapidement. Montrons que la fonction exponentielle est croissante : on a montré précédemment que la fonction exponentielle ne s'annule jamais. Donc 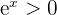D'où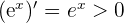 
Si la dérivée est positive, alors la fonction est croissante.
❌ Attention, croissante et positive sont deux choses tout à fait différentes et l'une n'implique pas forcément l'autre
Représentons la fonction exponentielle dans un repère :
On peut également réaliser le tableau de variation de la fonction exponentielle :
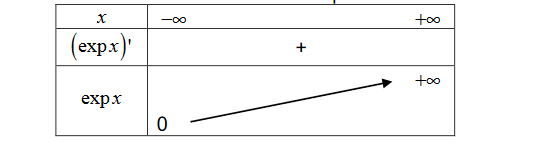
📚 Sa fonction réciproque est le logarithme népérien, noté ln, c'est à dire que 
- A l'inverse de la fonction exponentielle, la fonction logarithme est définie et continue sur [ ]0;+\infty [ ] et à valeur dans
Propriétés de l'exponentielle 🔢
La fonction exponentielle admet de nombreuses propriétés importantes qu'il est nécessaire de connaître : [e^1=e] qui vaut environ 2,72.
[exp(0)=e^0=1]
- Soient x et y deux nombres réels,
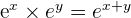et 
- On a de plus,
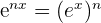
- Soit u une fonction définie et dérivable sur . La dérivée de la fonction
est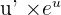 
où u' est la dérivée de la fonction u. De plus, la fonction u et la fonction ont le même sens de variation. - Pour tous réels a et b, on a
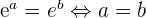et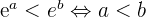 
car la fonction exponentielle est strictement croissante.
Limites de la fonction exponentielle 🤔
Déterminons les limites aux bornes de la fonction exponentielle.
Limite au voisinage +∞
👉 Pour cela, démontrons que pour tout x appartenant à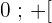 
, 
- Cela revient à démontrer que pour tout x appartenant à ,
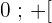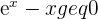
- Soit f la fonction définie sur
- La dérivée de la fonction f est
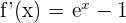
On a f’(x)=0 <=> exp(x)=1 <=> x=0 et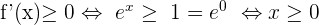 
- Donc f'(x) est strictement positive sur ]0 ; +∞[ ce qui implique que f est strictement croissante sur ]0 ; +∞[. Son minimum est atteint en 0 et f(0)=0.
- Donc pour tout x appartenant à [0 ; +∞[,
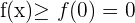ce qui équivaut bien à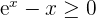 
Enfin, on a 
Limite au voisinage -∞
🙌 On sait que 
- On a
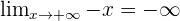d'où 
- Donc la limite de la fonction exponentielle lorsque x tend vers -∞ est 0.
D'autres limites concernant la fonction exponentielle sont à connaître. Par croissances comparées, on définit les limites suivantes :
De plus 
pour tout entier n. De la même façon,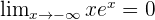 
De plus, pour tout entier n on a 
- On constate que la fonction exponentielle "l'emporte" sur la fonction identité (sur x).
- Énonçons une dernière limite à connaître
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !