Chapitres
- 01. Probabilité et indépendance
- 02. Espérance et variance d'une loi binomiale
- 03. Loi uniforme
- 04. Quelques définitions de base
- 05. La probabilité d'un événement
- 06. Réunion d'événements
- 07. L'événement contraire
- 08. L'équiprobabilité
- 09. Exercice d'application
- 10. Entraînement aux probabilités en maths

Probabilité et indépendance
Si on considère A et B comme deux événements, sachant que A est un événement de probabilité non nulle, alors on peut définir la probabilité de B sachant A par la formule suivante : 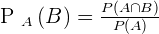 On appelle cela une probabilité conditionnelle car on veut connaître la probabilité de B en sachant que A s'est produit avant. Il est possible de dire de deux événements qu'ils sont indépendant si et seulement si la condition suivante est vérifiée :
On appelle cela une probabilité conditionnelle car on veut connaître la probabilité de B en sachant que A s'est produit avant. Il est possible de dire de deux événements qu'ils sont indépendant si et seulement si la condition suivante est vérifiée : 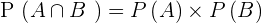
Espérance et variance d'une loi binomiale
En cour de math, il existe des formules afin de calculer l'espérance et la variance d'une telle loi. Si on définit X comme suivant une loi binomiale de paramètres n et p alors :  et
et  Avec :
Avec :
- E l'espérance ;
- et V la variance.
Loi uniforme
Il est possible de définir une loi uniforme sur [a ; b ] de la façon suivante (cours de maths terminale s):
| Fonction de densité sur [ a ; b ] | 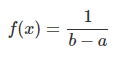 |
|---|---|
| Probabilité | 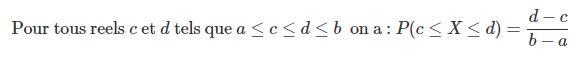 |
| Espérance | 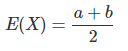 |
Quelques définitions de base

Expérience aléatoire
Une expérience aléatoire correspond à une expérience dont le résultat n'est pas prévisible de façon certaine. On peut ainsi prendre l'exemple du lancer d'un dé équilibré à 6 faces. En effet, il existe 6 résultats possibles dont aucun n'est prévisible de façon certaine (cours de maths seconde).
Issu d'une expérience aléatoire
Tout résultat possible de l'expérience est appelé issue d'une expérience aléatoire.
Univers

L'univers d'une expérience aléatoire, noté Ω, correspond à l’ensemble des issues possibles de cette même expérience. Toujours en prenant l'exemple du lancer d'un dé équilibré à 6 faces, l'univers correspond à Ω = { 1, 2, 3, 4, 5, 6 } Besoin de cours de math 3eme ?
Evénement
Un événement, noté A, correspond à une partie de l'univers Ω. Toujours dans l'exemple du lancer d'un dé équilibré à 6 faces, l'ensemble { 2, 4, 6 } correspond à un événement que l'on peut définir comme étant "obtenir un nombre pair".
Evénement élémentaire
Si Ω correspond à l'univers d'une expérience aléatoire, on considère un événement élémentaire comme étant tout événement qui ne comporte qu'une seule issue. Toujours en prenant l'exemple du lancer d'un dé équilibré à 6 faces, les événement { 1 }, { 2 }, { 3 }, { 4 }, { 5 }, { 6 } correspondent aux événements élémentaires de cet univers.
Evénements incompatibles
On dit de deux événements qu'il sont incompatibles s'il ne peuvent pas se produire de façon simultanées. De ce fait, ces deux événements ne contiennent aucune issue commune. Toujours en prenant l'exemple du lancer d'un dé équilibré à 6 faces, l'événement A : "obtenir la face 1" et l'événement B : "obtenir la face 3" sont considérés comme étant incompatibles puisqu'ils ne peuvent pas être réalisés de façon simultanée.
Evénement contraire
Un événement contraire à un événement A correspond à tout événement dont l'ensemble des éléments de l'univers Ω ne se trouvent pas dans A. Toujours en prenant l'exemple du lancer d'un dé équilibré à 6 faces, l'événement A : "obtenir un nombre pair" et l'événement B : "obtenir un nombre impair" sont considérés comme étant des événement contraires.
La probabilité d'un événement

Si A est un événement, alors on considère la probabilité de A, notée p(A), comme étant la probabilité égale à la somme des probabilités des événement élémentaires constitutif de l'événement A.
Evénement certain
On considère un événement certain comme étant un événement qui se réalisera obligatoirement. Ainsi, la probabilité de cet événement est égale à 1. Toujours en prenant l'exemple du lancer d'un dé équilibré à 6 faces, l'événement A : "obtenir un nombre compris entre 1 et 6" correspond à un événement certain.
Evénement impossible
On considère un événement comme étant impossible tout événement qui ne se réalisera jamais. De ce fait, sa probabilité est nulle. Toujours en prenant l'exemple du lancer d'un dé équilibré à 6 faces, l'événement A : "obtenir le nombre 8" est un événement impossible.
Réunion d'événements
Si A et B correspondent à deux événements de l'univers Ω, on appelle réunion de A et B tout événement noté A ∪ B comprenant les issues qui peuvent se réaliser dans un moins un des deux événements A ou B. On peut alors obtenir les théorèmes suivant :
Si A et B sont deux événements incompatibles, alors p(A ∪ B) = p(A) + p(B) Si A et B sont deux événements alors p(A ∪ B) = p(A) + p(B) - p(A ∩ B) ou encore p(A ∪ B) + p(A ∩ B) = p(A) + p(B)
L'événement contraire
Si A est un événement de l'univers Ω, alors la probabilité de son événement contraire est égale à 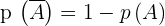 Il est important de savoir que :
Il est important de savoir que :
L'équiprobabilité
On considère une situation comme étant équiprobable tout expérience où tous les événements élémentaires de l'univers Ω ont la même probabilité d'être réalisés. Ainsi, dans l'exemple du lancer d'un dé équilibré à 6 faces, chaque face à la même probabilité de sortie. Cet exemple correspond donc à une situation d'équiprobabilité. De ce fait, en situation d'équiprobabilité, il est possible de connaître la probabilité d'un événement à grâce à la formule suivante : 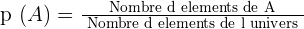
Exercice d'application

Dans un sac il y a 9 boîtes bleues, dont 6 contiennent un réglisse, et 3 boîtes vertes, dont 2 contiennent un jouet. B: "obtenir une boîte bleue" V: "obtenir une boîte verte" J: "obtenir un jouet" R: "obtenir un réglisse" 1. P(B) = ? 2. P(V) = ? 3. P(J) = ? 4. P(R) = ? 2. On tire une boîte au hasard dans le sac, on obtient une boîte verte; quelle est la probabilité qu'il y ait un jouet à l'intérieur? 3. On tire une boîte au hasard dans le sac, on obtient une boîte bleue; quelle est la probabilité qu'il y ait un jouet à l'intérieur? Corrigé: 1. P(B) = 9/12 = 3/4 2. P(V) = 3/12 = 1/4 3. P(J) = 5/12 4. P(R) = 7/12 2. Pv(J) = 2/3 3. Pb(J) = 3/9 = 1/3
Entraînement aux probabilités en maths
Exercice 1 : La loi binomiale
On jette 2 fois une pièce de monnaie. Cet acte à deux solutions possibles :
- La pièce s'arrête sur « PILE »
- La pièce s'arrête sur « FACE »
On note P le résultat « PILE » et F le résultat « FACE ».
1. Calculer p(P) et p(F)
2. Tracer l'arbre pondéré représentant l'issue de deux jets indépendants de la pièce.
3. Déterminer la probabilité d'obtenir deux fois FACE.
Exercice 2
On lance trois fois la même pièce de monnaie parfaitement équilibrée. On note X la variable aléatoire égale au nombre de «PILE» obtenus sur trois lancers.
1. Donnez la loi de probabilité de X
2. Calculer E(X)
3. Calculer V(X)
Exercice 3
On jette dix fois la même pièce de monnaie parfaitement équilibrée.
1. Quelle est la probabilité d'obtenir 5 fois pile ?
2. Quelle est la probabilité d'obtenir au moins une fois pile ?
Exercice 4
Une boîte contient 8 cubes (3 petits rouges et un gros rouge, deux gros vert et un petit vert, un petit jaune). Un enfant choisit au hasard trois cubes dans la boîte.
1. On note :
- A : l'événement d'obtenir trois cubes de couleurs différentes.
- B : l'événement d'obtenir au plus un petit cube.
a. Calculer la probabilité de A.
b. Calculer la probabilité de B.
2. Soit X la variable aléatoire donnant le nombre de gros cubes verts tirés par l'enfant.
a. Donner la loi de probabilité de X
b. Calculer E(X)
3. L'enfant répète n fois l'opération « Tirer au hasard trois cubes dans la boîte ». Les cubes sont remis dans la boîte après chaque tirage, et chaque tirage est indépendant. Déterminer Pn en fonction de n.
Correction de l'exercice 1
1. p(P) = ½ p(F) = 1- p(P) = ½
2. Il est nécessaire de faire un arbre pondéré
3. La probabilité d'obtenir deux fois le côté FACE est de ½ * ½ = ¼
Correction de l'exercice 2
1. On peut traduire la situation par un arbre pondéré.
Ainsi, chaque situation a pour probabilité: ½ * ½ * ½ = 1/8 X étant la variable aléatoire égale au nombre de PILE obtenus après 3 lancers de la pièce, alors X peut prendre pour valeurs 0, 1, 2 et 3. On peut donc donner la loi de probabilité de X :
2. Calcul de E(X) E(X) = 0*1/8 + 1*3/8 + 2*3/8 + 3*1/8 = 12/8 Donc E(X) = 3/2.
3. Calcul de V(X) V(X) = 0²*1/8 + 1²*3/8 + 2²*3/8 + 3²*1/8 – E(X)² = 3/4
Pourquoi ne pas demander de l'aide en cours de maths en ligne ?
Correction de l'exercice 3
Il s'agit d'un schéma de Bernoulli.
1. La probabilité d'obtenir PILE à chaque lancer est de 1/2. Ce schéma suit donc la loi binomiale de paramètre n = 10 et p = ½ La probabilité d'obtenir 5 fois pile est donc de :
2. Le contraire de l'événement “obtenir au moins une fois pile” est “ne pas obtenir pile”. Vu de cette façon, la réponse devient alors triviale.
Correction de l'exercice 4
Tous les tirages sont équiprobables. On note Ω l'ensemble des éventualités.
1. a) La probabilité A d'obtenir des cubes de couleur différentes est égale à :
Donc p(A) = 12 / 56 = 1 / 4
b) La probabilité d'obtenir au plus un petit cube est égale à :
Donc p(B) = 16 / 56 = 2 / 7.
2. X donne le nombre de petits cubes verts tirés par l'enfant. Or il y a 2 gros cubes vert au total dans la boîte. X peut alors prendre les valeurs 0, 1 ou 2.
On a alors :
b. Calcul de E(X) = 0x5/28 + 1*15/56 + 2*3/56 = 21/56
3. Les tirages sont indépendants. Il s'agit donc d'une loi binomiale de paramètre n et p = p(B) = 2/7. La probabilité que B ne soit réalisé aucune fois est :
La probabilité que B soit réalisé au moins une fois est donc de : Pn = 1 - (5/7)n























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Félicitations pour ce travail.
J’ai un petit problème avec les maths pouvez vous m’aider s’il vous plaît ?