Chapitres
- 01. Introduction
- 02. Définition
- 03. Exercices

Introduction
En mathématiques, il existe différentes méthodes pour démontrer une proposition ou une propriété. La récurrence est l'une d'entre elles. C'est une méthode simple qui permet de démontrer une assertion sur l'ensemble des entiers naturels.
Définition

La première question que l'on se pose est bien-sur : à quoi sert le raisonnement par récurrence ? Le raisonnement par récurrence sert à démontrer qu'une proposition est vraie pour tout entier naturel n. C'est l'une des méthodes de démonstration utilisées en mathématiques. L'ensemble des entiers naturels est noté N, il contient l'ensemble des entiers qui sont positifs. Après avoir énoncé la propriété que l'on souhaite démontrer, souvent notée P(n), on peut commencer notre raisonnement de démonstration. Il est composé de trois étapes : En premier lieu, on commence par l'initialisation : il faut démontrer que la proposition est vraie pour le premier rang, au rang initial. Très souvent, c'est pour n=0 ou n=1, cela dépend de l'énoncé. Dans un second temps, on applique l'hérédité : il faut démontrer que, si la proposition est vraie pour un entier naturel n, est vraie au rang n, alors elle est vraie pour l'entier suivant, l'entier n+1. C'est à dire,  L'hypothèse "la proposition est vraie au rang n" s'appelle l'hypothèse de récurrence. Enfin, la dernière étape est la rédaction de la conclusion : la proposition est vraie au rang initial et est héréditaire alors elle est vraie pour tout entier naturel n. Cette conclusion est toujours la même. Attention, avec ce raisonnement, on démontre une propriété uniquement sur N. C'est pourquoi on l'utilise principalement avec les suites. Ce raisonnement ne fonctionne pas pour une fonction où l'inconnue, x, est définie sur un autre ensemble que N, (par exemple sur R). Ce raisonnement va par exemple nous permettre de démontrer des égalités et des inégalités sur les entiers naturels ou sur les suites; Vous cherchez des cours de maths ?
L'hypothèse "la proposition est vraie au rang n" s'appelle l'hypothèse de récurrence. Enfin, la dernière étape est la rédaction de la conclusion : la proposition est vraie au rang initial et est héréditaire alors elle est vraie pour tout entier naturel n. Cette conclusion est toujours la même. Attention, avec ce raisonnement, on démontre une propriété uniquement sur N. C'est pourquoi on l'utilise principalement avec les suites. Ce raisonnement ne fonctionne pas pour une fonction où l'inconnue, x, est définie sur un autre ensemble que N, (par exemple sur R). Ce raisonnement va par exemple nous permettre de démontrer des égalités et des inégalités sur les entiers naturels ou sur les suites; Vous cherchez des cours de maths ?
Exercices

Afin de comprendre son utilisation, regardons différents exemples où le raisonnement par récurrence peut être utilisé. Souvent, on pourra remarquer que ce n'est pas la seule méthode de démonstration possible. Nous allons pour cela appliquer le raisonnement sur les suites dans différents cas.
- Soit la suite
 avec U_{0}=0 définie sur N.
avec U_{0}=0 définie sur N.
C'est une suite qui est définie par récurrence puisque Un+1 est exprimé en fonction de n. Nous allons démontrer par récurrence que pour tout n appartenant à N, on a 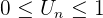 On note la propriété P(n) :
On note la propriété P(n) : 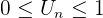 Initialisation : Pour n=0, on a
Initialisation : Pour n=0, on a  On a bien
On a bien  Donc la propriété est vraie pour n=0, elle est vraie au rang initial. On peut noté ça : P(0) vraie. Hérédité : On suppose que la propriété est vraie au rang n. C'est à dire, pour un entier naturel n,
Donc la propriété est vraie pour n=0, elle est vraie au rang initial. On peut noté ça : P(0) vraie. Hérédité : On suppose que la propriété est vraie au rang n. C'est à dire, pour un entier naturel n, 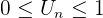 On veut démontrer que la propriété est vraie au rang n+1, c'est à dire
On veut démontrer que la propriété est vraie au rang n+1, c'est à dire  On a
On a 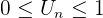 d'où
d'où  De même,
De même,  et
et 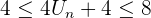 Ainsi,
Ainsi,  Finalement, on obtient
Finalement, on obtient  C'est à dire
C'est à dire 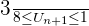 On a bien montré que
On a bien montré que 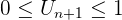 Donc la propriété est héréditaire. Conclusion : La propriété est vraie pour n=0, c'est à dire au rang initial et elle est héréditaire donc la propriété est vraie pour tout entier naturel n (cours de maths 3ème).
Donc la propriété est héréditaire. Conclusion : La propriété est vraie pour n=0, c'est à dire au rang initial et elle est héréditaire donc la propriété est vraie pour tout entier naturel n (cours de maths 3ème).
- Nous allons démontrer que pour tout entier naturel n>0, n(n+1)(n+2) est un multiple de 3.

Cela revient à montrer que pour tout entier naturel n>0, il existe un entier k tel que n(n+1)(n+2)=3k On note la propriété P(n) : n(n+1)(n+2)=3k Initialisation : Pour n=1, [ 1 x 2 x 3] ce qui est égal à 6. On a bien un multiple de 3. Il existe bien un entier k, ici k=2. La propriété est donc vraie pour n=1, au rang initial. Hérédité : Nous supposons que la propriété est vraie au rang n, c'est à dire n(n+1)(n+2)=3k, où k est un entier. Nous allons démontrer qu'il existe un entier k' tel que (n+1)(n+2)(n+3)=3k' c'est à dire que la propriété est vraie au rang n+1. On commence notre raisonnement par ce que l'on sait, ce qui est vrai : n(n+1)(n+2)=3k c'est à dire 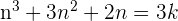 On a
On a 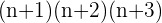
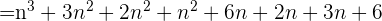
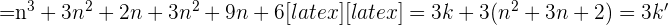 P(n)=>P(n+1), la propriété est héréditaire. Conclusion : La propriété est vraie au rang initial c'est à dire pour n=1 et elle est héréditaire donc la propriété est vraie pour tout entier naturel n positif.
P(n)=>P(n+1), la propriété est héréditaire. Conclusion : La propriété est vraie au rang initial c'est à dire pour n=1 et elle est héréditaire donc la propriété est vraie pour tout entier naturel n positif.
- Montrons que pour tout entier naturel n

Le symbole ci dessus représente la somme des entiers de 0 à n, c'est à dire 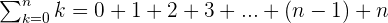

La propriété que l'on souhaite démontrer est P(n) :  Initialisation : Prenons n=0. La somme de k=0 à n=0 vaut 0. De même,
Initialisation : Prenons n=0. La somme de k=0 à n=0 vaut 0. De même,  Donc la propriété est vraie au rang initial, P(0) vraie. Hérédité : On suppose que la propriété est vraie au rang n, c'est à dire
Donc la propriété est vraie au rang initial, P(0) vraie. Hérédité : On suppose que la propriété est vraie au rang n, c'est à dire  Montrons grâce à l'hypothèse de récurrence que la propriété est vraie au rang n+1, c'est à dire
Montrons grâce à l'hypothèse de récurrence que la propriété est vraie au rang n+1, c'est à dire 


 Donc la propriété est vraie au rang n+1 sous l'hypothèse de récurrence. Ainsi, la propriété est héréditaire. Conclusion : La propriété est vraie au rang initial et est héréditaire donc elle est vraie pour tout entier naturel n. Enfin, regardons un dernier exemple où la récurrence est utile.
Donc la propriété est vraie au rang n+1 sous l'hypothèse de récurrence. Ainsi, la propriété est héréditaire. Conclusion : La propriété est vraie au rang initial et est héréditaire donc elle est vraie pour tout entier naturel n. Enfin, regardons un dernier exemple où la récurrence est utile.
Comment demander de l'aide en cours de maths en ligne ?
- Montrons que la suite définie par
 où [U_o=3] est décroissante.
où [U_o=3] est décroissante.
Cela revient à montrer que pour tout n,  On a
On a  On a besoin du signe de la différence pour connaître le sens de variation de la suite. On veut montrer que la suite est décroissante soit que
On a besoin du signe de la différence pour connaître le sens de variation de la suite. On veut montrer que la suite est décroissante soit que 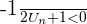 Cela équivaut à
Cela équivaut à 

On le montre par récurrence : Soit P(n) :  la propriété à démontrer. Initialisation : U0=3, On a bien U0>2. P(0) est vraie. Hérédité : On suppose que la propriété est vraie au rang n c'est à dire
la propriété à démontrer. Initialisation : U0=3, On a bien U0>2. P(0) est vraie. Hérédité : On suppose que la propriété est vraie au rang n c'est à dire  Montrons qu'elle est vraie au rang n+1 c'est à dire qu'on a
Montrons qu'elle est vraie au rang n+1 c'est à dire qu'on a 
 d'où
d'où 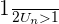 On obtient finalement
On obtient finalement  Donc la propriété est héréditaire. Conclusion : La propriété est vraie au rang initial c'est à dire pour n=0 et elle est héréditaire. Donc la propriété est vraie pour tout entier naturel n. Ainsi, pour tout n,
Donc la propriété est héréditaire. Conclusion : La propriété est vraie au rang initial c'est à dire pour n=0 et elle est héréditaire. Donc la propriété est vraie pour tout entier naturel n. Ainsi, pour tout n,  Donc
Donc 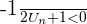 et la suite est strictement décroissante.
et la suite est strictement décroissante.





















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Bonjour, j’aimerai savoir si les informations ci dessus peuvent permettre l’obtention de plus connaissance en matière du sujet lui même en fonction de la quantité de connaissances déjà acquise tout en prenant en compte la quantité d’information de votre site
bon cours ça m’a beaucoup aidé
Bonjour , j’aimerais que vous m’aider car je n’arrive pas faire un exercice , j’aimerais que vous m’aider
Envoie moi l’exercice
Bonjour, nous sommes là pour ça, que souhaitez vous savoir ?
Salut je suis un bachelier et j’aimerais avoir 18de moyenne au bac alors si vous pouvez m’aider à me performer de plus je serais très ravis
Bonjour,
Grâce à Superprof, tu peux contacter de nombreux professeurs près de chez toi qui seront très heureux de t’aider à améliorer ton niveau.
T’as pris de l’avance sur le cours toi. Tu vas te balade mardi. =)